Page 270 - 1975_matematika-izium

Следовательно, если для двух из трех МНОГОУГОЛЬНIIКОВ Р, Р., Р!
Dеличнна т равна площади, то и для третьего справедливо то же
самое.
8СЯКI1ii МНОГОУГОЛЬНI1К с вершинамн в узлах решетки можно
разбить отрезками прямых на треУГОЛЬНI1КИ с тем же свойством. По-

.1 ........ j \
V \ V \

F, I
� :'.
/1. " " "-l"-
1\ � V
,
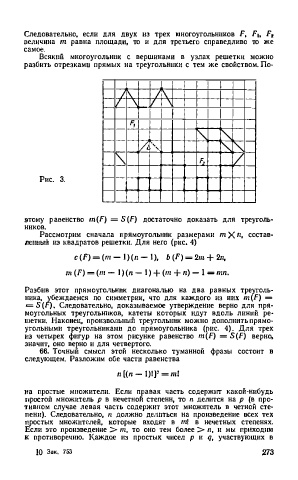
Рис. 3.

S
этому р а венство m(F) = ( F) достаточно доказать для треуголь­
ников.
Рассмотрим сначала ПРЯМОУГО!lЬНИК размерами т Х n, состав­
nеl1НЫЙ из квадратов решетки. Для него (рис. 4)
c (F) = ( m - I ) ( n - I ), Ь ( Е) = 2 m + 2 n,
т ( Р) = ( m - I ) ( n - I ) + ( m + n ) - 1 = m n.
Разбив этот прямоуго.%ЮIК диагона.'1ЬЮ на два равных треуголь­
ника, убеждаемся по симметрии, что для каждого из ннх m ( F) =
= S ( F), Следовательно, доказываемое утверждение верно для пря­
моугольных треугольюlКОВ, катеты которых идут вдоль линий ре­
шетки. Наконец, пронзвольный треУГОЛЬНIIК можно дополнить прямо­
угольными треугольниками до прямоугольника (рис. 4). Для трех
I!З четырех фигур на этом рисунке равенство m ( F) = ( F) верно,
S
значит, оно верно и для четвертого.
66. Точный смысл этой несколько туманной фразы состоит в
следующем. РаЗЛОЖIIМ обе части равенства
n [ (n - l)I]2 = m l
на простые множители. Если правая часть содержит какой-нибудь
IlрОСТОЙ МНОЖI!Тель р в нечетной степенн, то n делится на р (в про­
тивном случае левая часть содержит этот множитель в четной сте­
пени). Следовате.%но, n должно де.'lIlТЬСЯ на произведение Dcex тех
простых множитс.'1еЙ, которые входят в ml в нечетных степенях.
Если это произведенне > т, то оно тем более > n, и мы ПРIlХОДIIМ
К противоречию. I\аждое из простых чисе.1J р и q, участвующих в
10 3ак, 753 273